
트위터에서 @DrYoungjae 님이 올리신 ‘신박한 주차라인’ 사진을 보고, 문득 공간효율이 궁금해져서 간단히 계산해보았다. 다음은 그 계산 과정이다.
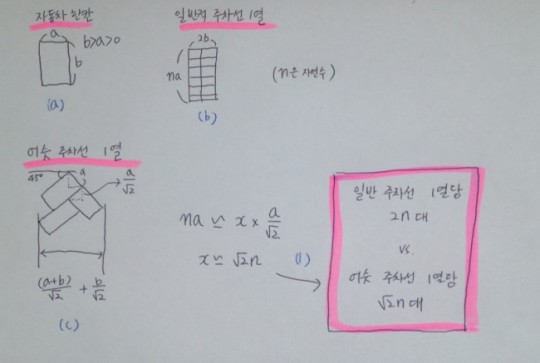
자동차 주차선 1칸의 가로 길이를 b, 세로길이를 a라고 하자. 그러면 일반적 주차선 1열의 모양은 그림 (b)와 같이 되고, 1열당 총 2n대가 주차된다.
이제 위 트위터 그림처럼 ‘어슷 주차선’을 생각해보자. (그림 (c)) 주차선을 45도 각도로 그려야 수직으로 잘 배열된다. 따라서 간단히 피타고라스 법칙을 이용해보면 가로 길이를 구할 수 있고, 세로방향으로는 주차선 하나 그릴 때마다 a/sqrt(2) 만큼 아래로 내려감을 알 수 있다.
이제 주차장이 아주 넓어서, 끝의 자투리 공간이 안 남아서 1~2대 분량 주차선을 못 그리는 정도는 큰 문제가 아니라고 가정하자. (10칸 대 9칸은 큰 차이지만, 10,000칸 대 9,999칸은 큰 차이가 아니다.)
그러면 일반적 주차선 1열을 그렸을 때 2n대의 차를 주차할 수 있다고 할 때, 어슷 주차선에 주차 가능한 자동차 대수 x는 식 (1)처럼 표현된다. 따라서 세로 길이가 똑같은 공간에서, 어슷 주차선을 그리면 1열당 sqrt(2) n대를 주차할 수 있다.

주차선을 1열만 그릴 것은 아니므로, 일반 주차선이 m열 들어가는 주차장을 생각하자. 그림 (d)에서 빗금영역은 일반주차선 1열을 뜻하고, 그 옆의 화살표 공간은 차량 통로를 뜻한다. 차량 통로의 폭은 kb라고 하자. (k > 1) 마찬가지로 주차장이 아주 넓다는 가정을 하면, 어슷 주차선 열 개수 y는 식(2)를 통해 구할 수 있다.
따라서 어슷 주차선으로 총 주차 가능한 차량 대수 xy 값은 식 (3)처럼 되고, a~= 0.4b (차량 폭이 길이의 약 40%라고 가정), k~=1.5라고 두고 계산해보면 1.55mn이라는 값이 나온다.
일반 주차선에서는 차량 2mn 대를 주차할 수 있으므로, 주차선을 어슷하게 그리면 공간효율이 떨어지는 셈이다. 그리고 주차장이 충분히 넓지 않으면, 자투리 공간을 딱 맞게 활용할 수 없어서 더 효율이 떨어질 수도 있다. 아마도 주차하는데 걸리는 시간은 절약되는 장점이 있겠지만, 서울처럼 땅값이 임금을 아득하게 넘는 곳에서는 절대로 채택될 수 없는 방식일 것이다.
그리고 난 이런 모양의 주차선을 한국에서도 몇 번 본적이 있다. 바로 제주도, 그리고 지방 고속도로 휴게소다. 우연일지는 모르겠지만 이곳은 땅값이 상대적으로 비싸지 않은 곳이다.
원문: cfr0g; 괴골 [개물]
