조엘 그린블라트의 『주식시장을 이기는 작은 책』은 정말 명저 중에 명저라고 할 수 있다. 한 줄로 요약할 수 있는 방법으로 계량 투자를 해도 미국 시장에서 20년간 연평균 수익률 40%를 거둘 수 있다니. 정말 읽고도 믿기지 않는다. 투자 관련 서적을 읽을 때 가장 중요한 것은 이 투자자가 실제로 어떤 성적을 거두었냐는 점이다. 슬프게도 대부분 서점에 가서 책을 보면 저자들이 ‘전업 저자’인 경우들이 많다. 실제로 우수한 트랙 레코드를 가진 경우는 극히 드물다.

조엘 그린블라트는 그런 저자들과는 차별된다. 실제로 펀드를 수십 년간 운영하기도 했고, 콜롬비아 비지니스 스쿨에서 강의를 하기도 했다. 감사하게도 성공한 투자자 중에 강의를 많이 하는 사람 중에 하나다.
백문이 불여일견.
이 책의 결론은 ‘마법 공식을 써라’라는 한 줄로 요약할 수 있다. 결론은 한 줄이지만, 이 책의 묘미는 한 줄을 한 권의 분량으로 설명했다는 데에 있다. 이 책은 마법 공식에 대한 책이라고도 할 수 있지만, 어떻게 계량적으로 투자를 해야 하는지에 대한 책이기도 하다. 이 책을 비롯하여 주변에서 마법 공식에 대한 좋은 얘기를 많이 듣다 보니 마법 공식으로 투자를 너무나 하고 싶어졌다. 하지만, 가장 큰 문제는 데이터를 제대로 만져보지 못했다는 것. 데이터를 직접 다뤄보지 않는다면, 전략에 대한 합리적인 자신감이 사라진다.
이건 마치 ‘연애를 글로 해봤어요’와 비슷한 거다. 연애에 대한 이론과 들은 얘기가 아무리 풍부해도 실제 해본 것과는 차이가 극심하니까. 합리적인 자신감이 없으면, 전략을 실행할 수 없다. 어떤 일이 생길지 어떻게 알까? 내일 당장 경제위기가 일어나면 어떻게 할까? 투자는 두려움과의 싸움이다. 이 두려움을 이겨내기 위해서는 실제 데이터를 다루는 경험이 필요하다.
마법 공식에 대해서 주변에 이것저것 물어보니 공통으로 들어오는 얘기가 신마법공식이 구마법공식보다 퍼포먼스가 좋다는 것이다. 아무리 다른 사람들이 얘기해도 내가 직접 데이터로 확인하기 전까지는 믿을 수가 없다. 그래서 필요한 데이터들을 구해보기 시작했다.
일봉/분봉/수급 정보 등으로 데이터베이스를 만들어놓기는 했는데, 재무제표는 아직 만들어보지 않았다. 이걸 처음부터 하는 것은 정말 귀찮은 일이었다. 데이터베이스를 만든다는 것은 과거 자료의 수집에서 시작하여 앞으로 새로운 자료를 업데이트하는 과정까지도 들어가니까. 아주 지루하고 힘든 시간이 있었으나 이런 디테일은 노잼일테니 간단히 생략한다.
하지만 데이터 모으는 시간 95 : 백 테스트 코딩하는 시간 5 정도의 비율이었고, 아마 대부분의 이 글을 읽는 사람들이 데이터를 모으지 못해서 백 테스트 하지 못할거라고 생각한다. 참 슬픈일이기도 하다. 데이터의 중요성은 아무리 강조해도 지나치지 않다. 투자가 노가다인 이유는 데이터를 끊임없이 정제하고, 수정하고, 구하고, 다뤄야 하기 때문이다. 각설하고, 일단 신마법공식이 더 쉬우니 신마법공식부터 보자.
신마법 공식
- GP / A = 매출총이익 / 총자본
- PBR = 주당순자산 비율이다 = 시가총액 / 자본이다.
각각에 대해 순위를 계산 후에 통합순위를 매기고, 통합순위가 낮은 순으로 매수하는 전략이다. 조금 유식한 표현으로는 멀티팩터 투자 방식이라고 하기도 한다. GP/A 는 퀄리티 팩터, PBR은 가격팩터. 신마법 공식의 6개월수익률을 계산하는 코드는 아래와 같다.
def get_return_new_magic(year, buy_month):
stock_finance = get_finance_new(year, buy_month)
stock_marketcap = get_stock_buydate(year, buy_month)
merge_df = pd.merge(stock_finance, stock_marketcap, on=’stockcode’)
merge_df[‘marketCap’] = merge_df[‘marketCap’] / 100000000
merge_df[‘gp_a’] = merge_df[‘매출총이익’] / merge_df[‘자산’]
merge_df[‘pbr’] = merge_df[‘marketCap’] / merge_df[‘자본’]
merge_df = merge_df.where(merge_df.pbr > 0 )
merge_df = merge_df.replace([np.inf, -np.inf], np.nan)
merge_df = merge_df.dropna()
merge_df[‘gp_a_rank’] = merge_df[‘gp_a’].rank(ascending=False)
merge_df[‘pbr_rank’] = merge_df[‘pbr’].rank(ascending=True)
merge_df[‘comb_rank’] = merge_df[‘gp_a_rank’] + merge_df[‘pbr_rank’]
stock_sell = get_stock_selldate(year, buy_month)
merge_df = pd.merge(merge_df, stock_sell, on=’stockcode’)
candidate = merge_df.nsmallest(BUY_LIMIT, ‘comb_rank’)
candidate[‘return’] = candidate[‘priceClose_y’] / candidate[‘priceClose_x’]
print(‘sum’, candidate[‘return’].sum())
return candidate[‘return’].sum() / BUY_LIMIT
구마법공식의 경우
자본수익률과 이익수익률을 가지고 순위를 매긴다.
자본수익률 = EBIT / (순운전자본 + 순고정자산)
EBIT 구하기가 힘들어서 그냥 GP(매출총이익)로 했다. 그래서 다시,
자본수익률 = GP / (( 유동자산- 유동부채) + (비유동자산 – 감가상각비))
아 감가상각비 계산해야 하는데, 이것까지 구하다가 지쳐서 일단 제외했다.
- 자본수익률 = GP / (( 유동자산- 유동부채) + (비유동자산 ))
이익수익률 = EBIT / EV(기업가치)
EBIT 는 그냥 GP로 대신하고, EV는 시가총액 + 총차입금 -현금성 자산 – 단기금융상품
단기금융상품 대신에 유동 금융자산으로 대체했다. 다시 정리하면,
- 이익수익률 = GP / (시가총액 + 총차입금 – 현금성 자산 – 단기금융상품)
이다. 이것도 똑같이 전 종목에 대해서 순위를 더하고, 그 순위의 합이 적은 순서대로 매수한다.
실제 전략을 백 테스트하면서 어려운 점들 중에 하나는, 내가 가진 데이터 중에서 팩터 전략에서 요구하는 데이터들을 대체할 수 있는 지식이 있어야 한다는 것이다. 슬프게도 fnguide 등에서 재무제표를 받다 보면 생략되는 경우가 흔하기 때문이다. 전체 대세의 흐름이 바뀌지 않는 선에서 단순하게 접근하는 것은 괜찮은 것 같다.
def get_return_old_magic(year, buy_month):
stock_finance = get_finance_old(year, buy_month)
stock_marketcap = get_stock_buydate(year, buy_month)
merge_df = pd.merge(stock_finance, stock_marketcap, on=’stockcode’)
merge_df[‘marketCap’] = merge_df[‘marketCap’] / 100000000
merge_df[‘자본수익률’] = merge_df[‘매출총이익’] / ( merge_df[‘유동자산’] + merge_df[‘유동부채’] + merge_df[‘비유동자산’] )
merge_df[‘이익수익률’] = merge_df[‘매출총이익’] / ( merge_df[‘marketCap’] + merge_df[‘장기차입금’] + merge_df[‘단기차입금’] – merge_df[‘현금및현금성자산’] – merge_df[‘유동금융자산’])
merge_df = merge_df.where(merge_df.자본수익률 > 0 )
merge_df = merge_df.where(merge_df.이익수익률 > 0 )
merge_df = merge_df.replace([np.inf, -np.inf], np.nan)
merge_df = merge_df.dropna()
merge_df[‘자본수익률_rank’] = merge_df[‘자본수익률’].rank(ascending=False)
merge_df[‘이익수익률_rank’] = merge_df[‘이익수익률’].rank(ascending=True)
merge_df[‘comb_rank’] = merge_df[‘자본수익률_rank’] + merge_df[‘이익수익률_rank’]
stock_sell = get_stock_selldate(year, buy_month)
merge_df = pd.merge(merge_df, stock_sell, on=’stockcode’)
candidate = merge_df.nsmallest(BUY_LIMIT, ‘comb_rank’)
candidate[‘return’] = candidate[‘priceClose_y’] / candidate[‘priceClose_x’]
print(‘sum’, candidate[‘return’].sum())
return candidate[‘return’].sum() / BUY_LIMIT
Colored by Color Scripter
그 외 백 테스트를 하며 여러 가정을 했다.
- 백 테스트
백 테스트 기간 : 2011년 6월부터 2018년 6월까지
상폐종목 제외(즉, 생존 편향이 존재함 )
거래세 제외(리밸런싱이 1년에 2번이기 때문에 큰 영향은 없을 듯)
배당소득 제외
리밸런싱시기 : 6월 1일, 12월 1일
– 6월 1일은 1분기 재무제표를 참고하고 함
– 12월 1일은 3분기 재무제표를 참고하고 함
아래는 백 테스트 메인 함수이다. 그냥 구마법공식인지 신마법공식인지를 구분해서 6개월마다 수익률을 계산하는 코드이다.
def magic(magic_type):
global equity
equity = pd.Series(0., index=rng)
money = 1
for year in range(2011, 2018):
for month_multiple in range(1, 3):
month = month_multiple * 6
cur_dt = date(year, month, 1)
print(year, month, ‘money’, money)
equity[cur_dt] = money
if magic_type == NEW:
money = money * get_return_new_magic(year, month)
else:
money = money * get_return_old_magic(year, month)
cur_dt = date(year + 1, 6, 1)
equity[cur_dt] = money
print(year + 1, 6, ‘money’, money)
ax.plot(rng, equity)
Colored by Color Scripter
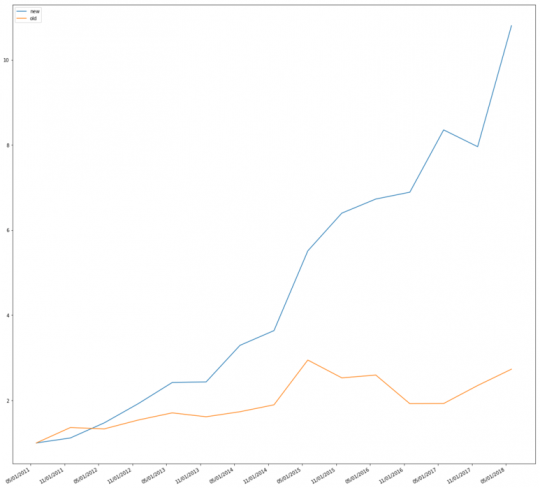
그래프에서 나오듯이 신마법공식(파란선)의 압승. 백 테스트는 근데 무엇을 어떻게 조금씩 바꾸냐 매수매도 시점을 언제로 설정하느냐 최근 분기를 반영하느냐 트레일링으로 반영하느냐에 따라 변수가 너무 많기는 하다. 그럼에도 불구하고 이 정도 차이면 꽤 큰 차이가 난다고 보는 게 맞다.
신마법공식 : CAGR 40%, 구마법공식 CAGR 15%
이 백 테스트 코딩하는 사이에 진이 빠져서 MDD까지는 계산 못했다. 이 백 테스트를 통해서 이젠 나도 ‘한국 시장에선 신마법공식이 더 잘 먹히네’라고 얘기할 수 있을 것 같다. 그리고 앞으로는 본격적으로 재무제표 데이터를 갖고 백 테스트해서 투자에 활용할 수 있게 된 것 같다. 야호.
※ 주의사항
* 이 결과는 생존 편향이나 각종 외부변수로 인해 차이가 있을 가능성이 큼.
* 과거 수익률은 미래 수익률을 보장하지 못함.
* 종목들 골랐는데 하루 거래량이 500만 원이라 거래가 사실상 불가능할 수도 있음.
원문: 투자스터디
