IoT 그리고 AI에 이어 비트코인 광풍이 불었다. 요즘은 코드도 공개가 되어 있고, 서적도 많고, 코딩스킬을 가지고 있는 사람들이 조금만 들여다보면 암호화폐류와 블록체인을 구현해볼 수가 있으니, 세상 참 좋아지긴 했다. 하긴 이 정도도 해보지 않은 이들이 너도 나도 전문가라고 떠드는 세상이다. 이 정도만 할 줄 안다고 하면 전문가라고 할 수 있을지도 모르겠다.
어쨌든 나 같은 알바생도 조그마한 관심만 있으면 얼마든지 배울 수 있으니 괜찮은 것 같다. 아, 그렇다고 내가 암호화폐류를 코딩하는 능력자는 아니다. 그냥 비트코인, 엄밀히 말하면 블록체인에 관심이 있는 사람일 뿐이다. 서두에서도 이야기했지만 요즘은 능력자도 많고 관련 내용도 많기에 비트코인을 비교적 쉽게 접할 수 있다. 사실 관련 자료가 너무나 많은 게 문제다. 그리고 대부분 구라가 많은 것 또한 사실이다.
비트코인을 이해하기 위해서는 「비트코인 백서(white paper)」로 알려진 문서를 알아야 한다. 아는 분은 아시겠지만 이 문서는 비트코인을 처음 제안한 사토시 나카모토(Satoshi Nakamoto)의 「비트코인: P2P 전자화폐시스템(Bitcoin: A Peer-to-Peer Electronics Cash System)」을 번역한 것이다.
물론 사용자의 입장에서 「비트코인 백서」를 모두 알 필요는 없다. 최근에는 이 백서를 잘 풀어서 설명한 자료도 많으니 이에 대한 설명은 생략하겠다. 사실 오늘 하려는 이야기는 수학에 관한 것이다. 「비트코인 백서」에서 보면 총 4개의 수학 공식이 나온다. 그중 핵심이 되는 공식은 2개(1번, 3번)이다. 오늘은 그중 한 가지 수식에 대해서 이야기를 풀어갈까 한다.
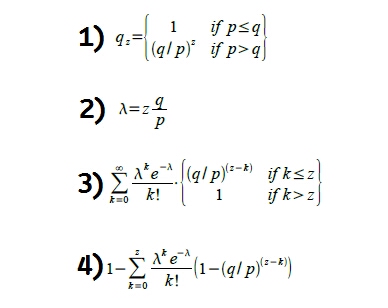
51% 공격에 대한 수학적 정리
여러분도 51% 공격(51% Attack)에 대한 이야기를 들어본 적 있을 것이다. 이에 대한 것은 여러 글에서 언급된 적이 많다. 51% 관련 글들을 보면 다음과 같다.
51% 공격(혹은 취약점)이라 함은 채굴이 가능한 노드 중 과반 이상이 공격 노드(혹은 장부조작을 하고자 하는 노드)인 경우 장부의 조작을 합법적으로 할 수 있다는 것이다. 즉 누군가가 채굴 노드의 과반 이상을 통제해 합법적으로 장부를 조작하는 공격을 뜻한다.
「비트코인 백서」에 나오는 수학 공식 이야기한다더니 갑작스럽게 51% 공격에 대한 이야기로 시작해서 조금 당황했을지 모르겠다. 아시다시피 「비트코인 백서」에는 51% 공격과 직접 연결된 내용은 없다. 또 하나, 「비트코인 백서」를 자세히 설명한 자료가 많기는 하지만 유독 한 부분에 대한 설명을 찾기가 어려운데, 그건 바로 PoW에서 등장하는 수학 공식에 대한 설명 부분이다. 그리고 여기에 처음 등장하는 수식이 있다.
「비트코인 백서」의 내용을 살펴보자

「비트코인 백서」에 처음 등장하는 이 수식이 중요한 이유는 바로 이 부분이 51% 공격과 직접적인 연관이 있기 때문이다. 일단 이 부분은 조금 읽기 쉽게 정리해 보았다.

사실 위의 식은 원래 있던 공식을 다시 정리한 것뿐이다 . 다만 변수를 조금 바꾸었고, 변수에 대한 추가적인 설명을 했다. 위의 수식을 보는 방법은 다음과 같다.
- q_0는 공격자(attacker) 노드가 현재 장부를 완료한 시점에서 그다음 장부를 합법적으로 조작(더 정확하게 말하자면, 다음 장부를 합법적으로 수정하는 것을 의미)할 수 있는 가능성(확률)을 의미한다.
- p_0는 합법적인 노드가 현재 장부(0)를 완료한 시점에서 다음 장부(0+1)에 합법적으로 수정(혹은 기입)할 가능성을 의미한다.
- 다음노드(0+1)의 입장에서는 정확한(혹은 정직한) 장부로 완료가 되거나, 공격자에 의해 거짓된 장부로 완료되거나 둘 중 하나가 된다(즉 그 중간은 없다). 이를 수학적으로 표현하면, p_0 = 1-q_0
- 만약 현재 장부가 아닌 h만큼 과거에서 다음 장부(0+1)를 조작되어 완료될 할 가능성은 q_h가 된다.
- 만약 공격(혹은 추월)을 해야 할 장부가 그다음 장부(0+1)에서 꽤 떨어져 있다면(h가 상대적으로 큰 수), 다음 장부가 공격(혹은 조작)당할 가능성은 0(zero)에 수렴한다 (h가 무한대).
- q_h는 공격자가 h개의 장부만큼 떨어진 시점에서 그다음 장부(0+1)를 조작할 가능성(확률)을 의미한다.
아마 위의 내용은 「비트코인 백서」를 나름 잘 분석한 분이라면 아실 만한 내용일 것이다. 하지만 조금만 더 설명해보도록 하겠다.
- h개만큼의 과거(혹은 뒤 쳐진 장부)에서 다음장부(0+1)가 정상적인 장부로 완료 될 가능성은 p_h=1-q_h
- 현재 장부를 완료한 시점에서 공격자 노드(q_0)와 정상 노드(p_0)의 비율은 채굴 가능한 노드들 중에서 정상 노드와 공격자 노드의 비율과 동일 하다. 예를 들어 100개의 채굴 노드가 있다고 했을 때 65개가 정상적인 노드라면 p_0=0.65, q_0=0.35가 된다.
- 51% 공격에서 “51%”는 바로, p_0<=q_0인 경우를 의미한다.
- 하지만 (위의 수식 상으로) 더 엄밀하게 말하면 51%가 아니라, 50(+)%를 의미한다. 즉 50%보다 조금만 더 높아도 소위 말하는 “51% 공격”을 당한다.
- 실제로 51% 공격을 당할 가능성은, 공격 노드가 과반이 되지 않더라도 존재한다(수식의 두 번째 조건).
- 실제 다음 장부가 조작될 가능성은 현재 (초기)상태(0)의 정상 노드와 공격 노드의 비율을 의미할 뿐만 아니라, 만들어질 다음 장부(0+1)까지의 거리 (h)에 의해 결정된다.
아무래도 (11)과 (12)에 대해서는 조금 더 설명이 필요할 것 같다. 많은 사람이 정상 노드의 수가 공격 노드의 수보다 클 경우 안전할 거라고 생각한다. 하지만 위에도 언급했듯 설령 정상 노드가 공격 노드의 수보다 크더라도, 즉 정상 노드가 과반을 넘더라도 여전히 장부조작의 가능성이 존재(11)한다. 정상 노드가 과반이 넘을 경우에 그다음 장부(0+1)가 정상적으로 만들어질 가능성은 조작된 장부와 그다음 장부 사이의 거리에 의해 결정된다.
예를 들어 정상 노드가 전체 노드의 80%라도 그다음 만들어질 장부에서 2단계가 뒤처져 있다면(즉 이 경우 실제로 추월해야 할 장부는 현재 장부(0) 한 개(h=1)임을 뜻함) 공격 노드를 통해 그다음 장부가 조작될 가능성은 여전히 25%(20/80) 존재한다. 하지만 추월해야 할 장부의 수가 많을 경우는 그다음 장부가 조작될 가능성은 0에 가깝다.
- 만약 초기에 공격 노드의 수가 정상 노드의 수보다 많거나 같을 경우(즉 q_0 >= p_0), 그다음 장부(0+1)는 반드시 조작된 장부다(수식의 첫 번째 조건).
- 만약 공격자 노드가 추월해야 할 장부가 없을 경우 (혹은 현재의 장부(0)가 조작된 채로 완료가 되었을 경우) 정상 노드와 공격 노드의 비율에 관계없이 그다음 장부(0+1)는 무조건 조작된 장부로 만들어진다 (즉 h=0인 경우).
재미있는 점은 위에 언급된 1-14번 모든 이야기가 「비트코인 백서」에 언급된 수학 공식 중 한 개에서 나온 것이라는 점이다. 즉 공식 하나를 제대로 이해하면 위에 언급된 내용을 모두 파악할 수 있다는 뜻이기도 하다. 수학이라는 것이 이래서 유용하다. 나 같은 비전공자에게라도 말이다.
잠시 쉬어가는…
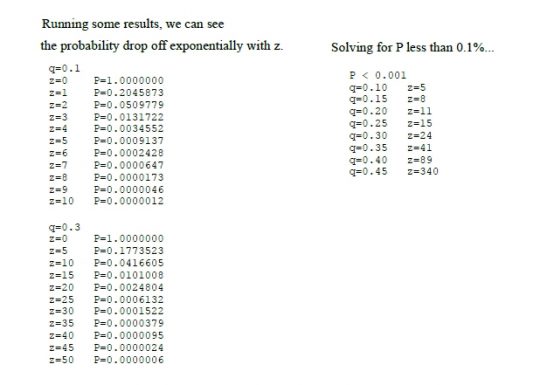
시작에도 언급했지만 비트코인에 언급된 수학 공식은 총 4개이다. 지금까지 다룬 것은 그중에 가장 첫 공식이고, 나머지 3개(2~4번)가 남았다. 백서의 내용에서 찾아보면 다음과 같다.

사실상 아래 두 공식은 한 개(같은 공식)고 가장 위 공식은 조건이다. 이제 나머지 공식들에 대한 이야기를 나눌 것이다. 그리고 백서에 언급된 코딩 결과물에 대한 이야기도 나눠 볼까 싶다.
계속 수학 공식 이야기를 하자
앞에서는 첫 번째 공식에 대해서 이야기했다. 이제 2~4의 수학 공식을 이야기하려고 한다. 우선 공식들을 설명하기 전에 우선 알아야 할 것이 있는데, 정리하자면 다음과 같다.
- 백서에서는 포아손 분포(Poission Distribution)를 이야기하지만 사실상 포아손 프로세스(Poission Process)를 의미한다.
- 분포와 프로세스의 가장 큰 차이점은 시계열성(Time Series)의 여부다.
- 분포는 단순한 확률이지만 프로세스는 확률모델(Stochastic Process)이다.
- 물론 수식 상으로 포아손 확률과 포아손 프로세스는 한 끗 차이다.
- 현재 장부가 공식적으로 확정된 시점부터 그다음 장부가 확정될 때까지 새로 만들어지는 장부의 확정을 기준으로 가능성(확률)을 계산하기 때문이다.
- 프로세스를 단순한 분포로 다룰 수 있는 이유는 시계열의 모델(Stochastic Model)이라고 하더라도, 확률의 계산은 “한순간”을 다루기 때문이다.
- 이러한 “한순간”을 시간순으로 엮으면 시계열, 혹은 Stochastic Process가 된다.
- 우리가 최종적으로 분석하고자 하는 것은 “공격자가 그다음 장부를 조작된 채로 만들어질 가능성(확률)의 기댓값(Expected Value)”이다.
- 블록체인 백서에서 다루는 장부생성에 관한 모델은 도박이론(Gambler’s Ruin Problem)을 기반으로 하지만 구하는 값은 공격자가 성공할 확률(즉 정상 노드가 실패할 할 확률)을 다룬다.
- 참고로 도박이론에서는 도박꾼이 돈을 벌 확률 확률(즉 블록체인에서 정상적인 노드의 장부가 확정될 확률)을 다룬다.
블록체인과 확률모델
다시 백서의 내용을 보자.

위의 공식을 지난번처럼 조금 더 쉽게 풀어 써보겠다. 우선 첫 번째(2번) 공식은 다음과 같이 풀 수 있다.

위의 수학 공식(및 조건)들을 설명하자면 다음과 같다.
- 우리가 원하는 분석을 하기 위해서 기본적으로 정상 노드(honest nodes)가 다음 장부가 확정되기 전까지 새로 만들어진 블록(혹은 장부)의 수는 항상 정해져 있고, 알고 있다고 가정한다 (h가 정해짐).
- 이후 공격자에 대한 확률적 분석은 이 전제를 기반으로 한다.
- 반면 공격자 노드에 의해 평균적으로 만들어지는 장부(블록)의 수는 정상 노드와 공격자 노드에 따라 결정 된다.
예를 들어 정상 노드(p_0)가 0.65, 공격자 노드(q_0)의 비율이 0.35라고 했을 때 정상 노드가 만드는 블록의 수가 650개라고 하면 공격자가 만드는 블록의 평균 갯수(λ_q)는 350개가 된다.
- 여기서 중요한 것은 실제로 공격자가 만드는 블록의 정확한 수(X)는 알 수가 없으나 포아손 분포를 따른다.
- 계산한 값(λ_q)은 공격자가 만드는 평균 장부의 수는 포아손 분포의 인자(factor)가 된다.

아까와 마찬가지로 수학적으로 보기 편하도록 위의 공식을 풀어 쓰자면 다음과 같다.
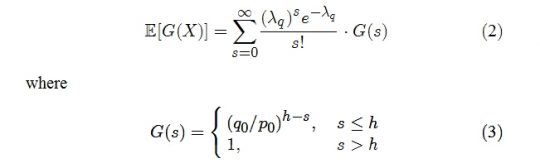
백서에 있는 수식은 2식이다. 그리고 이 수식은 두 개의 수식으로 구성되어 있다. 보기 편하게 G(X)라는 함수로 나누었다. 그렇다, G(s)가 아니라 G(X)이다. 그렇다면 G(X) 함수와 G(s)의 관계는 바로,

가 된다. 우선 3식에 대한 설명을 하도록 하겠다.
- 공식적으로 장부가 확정된 이후, 그다음 장부가 확정될 때까지 정상 노드가 만들어지는 장부의 수가 h이고, 같은 주기동안 공격자가 만든 장부의 수를 s라고 하면, 공격자가 그다음 (확정될) 장부를 조작하기 위해 추월해야 할 장부의 수는 h-s가 된다.
- 그리고 h-s만큼 떨어진 공격자의 장부로 그다음 장부를 조작할 가능성(확률)이 3식이다.
- 여기에 공격자 노드(attackers)와 정상 노드(honest nodes)의 비율(q_0, p_0)을 알고 있다면, 공격자 노드의 그다음 장부 조작의 가능성(확률)이 바로 3식이다(3식 첫 번째).
- 만약, 한 주기 동안 만들어내는 공격자의 장부의 수가 정상 노드가 만들어내는 장부의 수보다 큰 경우(X>h) 그다음 만들어지는 장부는 무조건 조작된 장부, 즉 공격자에 의해 만들어진 장부다(3식 두 번째).
- 공격자가 만드는 장부의 숫자는 X고 random variable이다. s 또한 공격자가 만드는 장부의 숫자이다. 이 두 인자(X, s)는 같기도 하고, 다르기도 하다. 이에 대한 정확한 차이를 알고 있다면, 당신은 확률론에 대해 상당한 내공을 가지고 있다는 의미이다.
공표(announce)되는 장부가 서로 다를 때 어느 장부가 정상인지 판단하는 방법에 관한 이야기를 들은 적이 있을 것이다. 다들 아시겠지만 공표되는 장부가 다를 경우 가장 긴 장부가 최종적으로 확정된다. 이 경우 공격자가 정상 노드보다 성능이 월등한 컴퓨터로 더 많은 장부를 생성한다면 100% 합법적으로 조작된 장부가 확정이 되는 이유가 바로 여기에 있다(17번 참고).
- 블록체인의 분석은 정상 노드로부터 만들어진 장부의 숫자는 정해진 것(h; deterministic)으로 가정하고, 공격자가 만든 장부의 숫자는 불확실한 것(X; random)으로 가정한다.
이제 마지막 수식 4를 살펴보자. 백서의 내용은 다음과 같다.
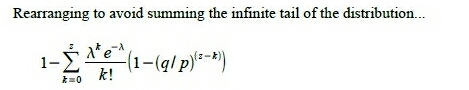
이를 이전처럼 수학적으로 조금 더 쉽게 적어보면,
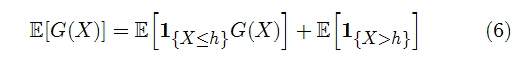
- 이 수식은 사실 수식 3과 “정확하게” 동일한 수식이다.
조금만 힌트를 주자면, 6식을 다음과 같이 전개할 수 있다.
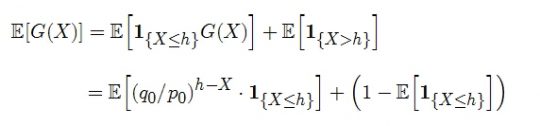
이 이후의 전개 방법은 독자 여러분께 맡기도록 하겠다.
마치면서…
적다 보니 이렇게 되었다. 다행히도 블록체인 백서의 수식이 그렇게 많지 않아 이 정도에서 마무리가 된 것 같다. 수학이 가지는 가장 큰 장점 가운데 하나는 말로 길게 설명해야 할 것을 단 몇 줄로 요약 가능하다는 점일 것이다.
물론 수식을 제대로 이해하기 위해서는 수식에 있는 각각의 문자가 가지는 의미를 정확하게 알아야 한다. 수식에 있는 문자들의 의미를 제대로 이해한다는 것은 엄밀한 의미에서는 수학의 영역이 아닐지도 모른다. 하지만 수학도 “읽고 쓰기”가 중요하기에 익숙해지면 엄청 유용하다. 다른 언어들처럼 말이다.

원문: Amang Kim의 브런치
