안녕하세요, 상당히 자극적인 제목으로 글을 시작했습니다. 다만 몇 가지 조건을 추가하면 해당 제목은 자극적인 제목이 아니라 지극히 합리적인 제목이 됩니다. 첫 번째는 ‘단기간에’라는 조건입니다. 그리고 두 번째는, 사실 이미 제목에 녹아 있는 말입니다만 ‘자본금이 충분히 크지 않다면’이라는 조건입니다.
두 번째 조건이 사실 이미 제목에 녹아 있다고 표현한 이유는, ‘자본금이 충분히 크다면’ 이미 당신은 부자이기 때문에 부자가 ‘될 수는’ 없기 때문입니다. 그러면 자극적인 제목을 합리적인 제목으로 바꾸기 위한 조건은 말씀드렸고, 오늘 나누고 싶은 이야기에 대해서 다뤄보겠습니다.

이야기를 전하기에 앞서서 가장 먼저 해야 할 것은 ‘부자’라는 추상적인 의미를 구체화하는 것이라고 생각합니다. 초록색 검색창에 검색을 해보면 이런저런 기준이 나옵니다만 기본적으로 ‘부자’라는 것은 상대적인 개념입니다. 그리고 공통적으로 부자가 되고 싶은 현재의 내 재정 상태와는 거리가 먼 재정 상태를 의미합니다.
즉 사람마다 ‘부자’의 기준은 다르지만 분명한 것은 현재 내 자산 규모보다는 훨씬 큰 자산 규모를 의미한다는 것입니다. 그래서 우리는 단기간에 투자로 부자가 될 수 없음을 인정하시라는 말을 전하고자 합니다.
금융은 기본적으로 변화’율’의 세계입니다. 산술급수가 아니라 기하급수(등비급수)의 단위로 움직입니다. 기하급수는 상당히 매력적인 개념입니다. 첫째 항에 일정한 숫자를 더함으로써 커지는 개념이 아니라 일정한 숫자를 곱함으로써 커지는 개념이기에 조금만 시간이 지나면 금방 어마어마한 숫자로 커집니다.
하지만 기하급수는 두 가지 값에 크게 영향을 받습니다. 우선 첫째 항의 값입니다. 첫째 항의 크기가 상이하고, 공비가 동일한 두 개의 기하급수는 똑같은 시간이 지났을 때 해당 단계의 항의 값 차이가 ‘기하급수적’입니다. 수열 자체가 기하급수(등비급수)이기 때문입니다.
또 크게 영향을 받는 값은 바로 공비입니다. 첫째 항의 크기가 동일하고 공비가 상이한 2개의 기하급수는 똑같은 시간이 지났을 때 해당 항의 값의 차이가 기하급수적입니다. 첫째 항이 2, 공비가 2인 기하급수의 100번째 항의 값과 첫째 항이 2고, 공비가 4인 기하급수의 100번째 항의 값은 어마어마한 차이가 납니다.

이런 기하급수의 수학적 특징이 제가 오늘 공유하고 싶은 잡상의 주제입니다. 금융의 세계에 진입한 우리에게 있어서 첫 번째 항은 자본금, 공비는 CAGR, 그리고 각 항은 각각 시간의 흐름에 따른 우리의 자산 가치를 의미합니다. 앞에서 정리한 기하급수의 수학적 특징을 적용시켜보면 우리의 각 시간에 따른 자산 가치는 자본금의 규모와 CAGR의 크기에 의해 결정됩니다.
그런데 앞에서 언급했다시피 ‘부자가 되고 싶은’ 우리의 현재 재무 상태는 충분히 큰 자본금을 갖추고 있지 못합니다. 충분히 큰 자본금을 갖추었다고요? 그럼 이미 부자이신 겁니다. 자본금의 크기도 상이하지만 부자라는 기준도 상이하기 때문입니다. 자신이 갖춘 자본금이 충분히 크다고 생각하면 자본금의 절대적인 크기가 상당하거나 부자라고 생각하는 자본의 절대적인 규모가 크지 않은 것이니까요.
따라서 ‘부자가 되고 싶은’ 우리는 충분히 큰 첫째 항을 가지고 시작하지 못합니다. 그러면 공비에 눈을 돌려야 합니다. 그런데 앞에서 말씀드렸다시피 금융은 변화율의 세계입니다. 즉 공비를 크게 하는 것은 자본금의 규모가 작은 나뿐 아니라 자본금의 규모가 어마어마한 워런 버핏이나 블랙록 같은 고래들에게도 매우 중요한 목표라는 것입니다. 그 말인즉슨 무엇일까요? 네, 쉽지가 않다는 것입니다.
공비를 키우는 것은 자본금을 키우는 것보다 더 힘들면 힘들지 쉽지가 않습니다. 결국 우리가 할 수 있는 것은 무엇일까요? 이미 첫째 항은 고정이 되어 있고, 공비는 아무리 노력을 해도 일정한 수준 이상으로 키울 수가 없습니다. 그런데 큰 자본을 갖고 싶기는 합니다. 아직 건드리지 않은 변수가 하나밖에 더 있나요? 시간입니다. 내가 부자라고 할 수 있을 만한 자본 규모를 갖추는 항을 뒤의 항으로 충분히 잡는 수밖에 없습니다.
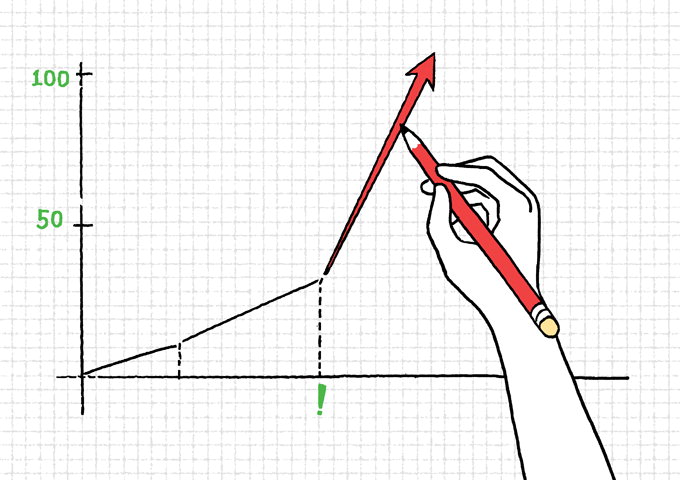
다행스럽게도 기하급수의 세계는 자비로워서 첫째 항의 크기가 엄청나지 않아도, 공비의 크기가 비현실적이지 않아도, 항의 순서만 충분히 뒤로 미룬다면 우리에게 ‘부자라고 할만한 자본’을 안겨줍니다. 이런 기하급수의 자비로움을 만끽하기 위해서 우리가 꼭 지켜야 하는 것이 있습니다. 바로 중간에 공비를 0으로 바꾸거나 큰 마이너스 값을 바꾸지 않는 것입니다.
수학은 절대적이고 완전해서 공비를 우리가 결정하면 그것이 곧 공비가 되지만 금융시스템에서 우리의 공비는 우리가 절대적으로 결정하기가 어렵습니다. 하지만 무슨 짓을 해서라도 공비가 0이 되거나 마이너스 값이 되는 일은 피하려고 노력해야 합니다. 그래야 우리는 기하급수의 자비로움을 만끽할 수 있기 때문입니다.
쉽지가 않지요? 네, 세상에 쉬운 일이 어디 있겠습니까? 하지만 공비를 0이나 마이너스 값이 되지 않게 하는 첫걸음은 “우리는 투자로 단기간에 부자가 될 수 없다”라는 사실을 인정하는 것이 아닐까 싶습니다. 단기간에 페라리를 타려고 하다가 가까운 곳의 그랜저도 잃어버리는 경우가 더러 있어서 말입니다. 가벼운 잡상이었습니다. 감사합니다.
원문: DB_
