
얼마 전까지 연재했던 AI의 핵심 인재에 관한 글에 보낸 관심에 감사를 드린다. 정작 AI에 관련한 글을 적으면서 AI를 빼고 이야기했음에 많은 분이 관심을 가져주셨다. 이번 이야기는 어쩌면 지난 글의 연장선이라 할 수도 있을 것이다. 몇 달 전인 듯하다. 페북을 통해서 다음과 같은 기사가 들어왔다.
- 「‘코딩’ 가르쳤더니 수학 실력이 ‘쑥쑥’」, 《사이언스타임즈》
- 「4차 산업혁명 대비 ‘코딩’ 교육 의무화…장·단점 알아보니」, 《노컷뉴스》
- 「유아까지 코딩 열풍…SW수업 의무화에 사교육시장 ‘꿈틀’」, 《연합뉴스》
논조의 차이는 있지만 미래를 대비하기 위해, 그리고 수학적(혹은 논리적) 사고를 키우기 위해 SW 교육(혹은 코딩 교육)을 어려서부터 할 필요가 있다는 이야기가 주류를 이룬다. 이에 관한 이야기를 수열(Sequence) 및 약간의 코딩(Pseudocode)을 예를 들어 이야기해 보도록 하겠다. 오늘의 코딩 문제는
- 1부터 10까지의 합을 구하는 코딩(혹은 프로그래밍)을 하시오.
- (1번에서 나온 답을 이용하여) 11부터 20까지의 합을 구하는 코딩을 하시오.
- 1부터 n까지의 합을 구하는 코딩을 하시오.
이다. 과연 여러분이 코딩한다면 어떤 식으로 할 것인가?
합을 구하는 코딩
여러분이 코딩을 조금 안다고 가정하고 바로 코딩으로 설명하겠다. 참고로 나는 코딩을 전문적으로 하는 사람은 아니다. 그냥 조금만 할 줄 아는 사람일 뿐이다. 그렇지만 오늘의 예제는 기본적인 코딩 지식만 있으면 쉽게 이해가 가능하리라. 여러분의 기본적인 소양을 믿고, 이 주제로 코딩 예제를 드려보고자 한다.
1부터 10까지 합
보통 이와 같은 문제를 코딩하면 크게 두 가지 방법으로 가능하다.
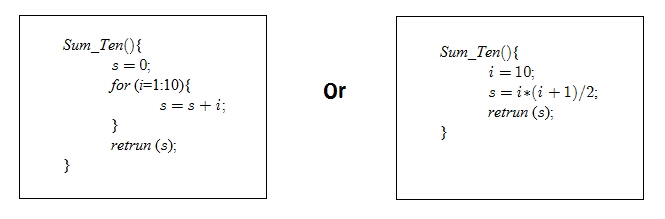
둘의 코딩을 비교해보면 라인 수는 비슷해보이지만 알고리듬의 복잡도를 봤을 때는 엄청난 차이를 보인다. 하지만 그보다 근본적인 차이는 왼쪽의 코딩은 등차수열 공식을 모르는 사람이, 오른쪽의 코딩은 등차수열 공식을 아는 사람이 짠 코드라는 것이다.
1부터 20까지 합을 구하는 코딩
몇 가지로 다르게 코딩이 가능하다. 코드를 보자.

가장 왼쪽 코딩과 가장 오른쪽 코딩은 위와 비슷하게 분석이 가능하다. 즉 왼쪽은 등차수열을 모르는 사람이, 오른쪽은 등차수열을 아는 사람이 짠 것이다. 중간 것은 어떤가? 복잡도 측면에서는 오른쪽 것만큼 우수하지만 여전히 등차수열 공식을 모르는 사람이 코딩한 것이다.
1부터 n까지 합을 구하는 코딩
n까지의 합을 구하는 코딩은 처음 1부터 10까지의 합을 구하는 코딩과 거의 유사하다.
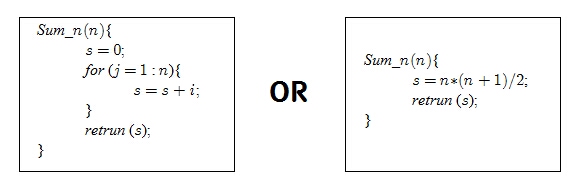
두 코드 사이의 차이는 위에서 언급했지만 알고리즘의 효율(복잡도의 측면)로 봤을 때라도 왼쪽 코드보다는 오른쪽의 코드가 훨씬 우수하다. 오른쪽 코드가 왼쪽 코드보다 복잡도 면에서 나은 이유를 모르겠다면 전산학과의 알고리즘(Algorithm) 과목을 참고하시라.
코딩을 하는 사람이 등차수열 지식이 있다면 더욱 효율적인 코딩을 할 수 있다. 하지만 등차수열 자체를 코딩에서 배우지는 않는다. 코딩을 배우면서 익힐 수 있는 것은 ‘어떻게(코딩)’일 것이다. 하지만 ‘어떻게(코딩)’만큼 중요한 것이 ‘무엇을(목적)’이다. ‘무엇을’의 내용은 여러분이 코딩이 아는 다른 곳, 즉 코딩을 뺀 곳에서 찾아야만 한다. 위의 예제에서는 왼쪽은 ‘어떻게’만 가지고 코딩한 것이고 오른쪽은 ‘무엇을(등차수열)’을 가지고 코딩한 것이다.
물론 왼쪽 같은 코딩 자체를 익숙하게 하는 데는 많은 시간과 노력을 들여야 한다. 일단 익숙해지고 나면 여러분이 어떤 일을 하든지 코딩의 도움을 받을 수 있을 것이다. 하지만 코딩(어떻게)에서 무엇(목적)자체를 배울 수는 없다. 마치 코딩을 배운다고 해서 등차수열(공식)자체를 배울 수 없는 것과 마찬가지이다. 등차수열(공식)을 모르더라도 코딩은 가능하니까 말이다.
‘어떻게’ ‘무엇’보다 중요한 것
조금만 물러나서 생각해보라. ‘위의 코딩 문제에서 가장 핵심이 되는 것은 등차수열 공식이란 말인가?’라는 의문이 생길 수도 있다. 그 대답은 ‘아니오’다. 등차수열 공식 자체보다 중요한 것은 등차수열 공식 자체의 검증, 즉 ‘왜’ 저 공식이 타당한지, ‘왜’ 일반적으로 적용할 수 있는지 아는 것이다.
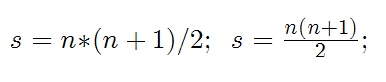
위의 공식 자체가 맞는 것인지 판단하는 것, 위의 공식이 왜 맞는지 원리를 찾아 가는 것이 코딩으로 문제의 답을 구하는 것이나 기본 원리를 단순히 알고 있는 것(등차 수열공식을 외우는 것)보다 훨씬 중요하다.
교육에서 코딩이 빠져야 하는 이유
글을 쓰는 중간에 잠깐 언급을 했지만 코딩 자체가 익숙해지면 어떤 일을 하든지 코딩의 도움을 받을 수 있다. 하지만 어려서부터 코딩만 집중하면 무엇(목적)을 고민할 수 없고, 더 나아가서는 ‘왜’에 대한 고민은 더더욱 할 수 없다. 단순한 기술 습득의 문제가 아니라 가치관의 문제이기도 하다.
특히 어릴 때 코딩 교육에만 집중하면 과학적·수학적 이론의 사실성 여부를 코드의 구현이나 실행 여부로 판가름하는 성향이 강해진다. 즉 어떤 과학적·수학적 사실이 컴퓨터를 통해 구현되면 참(사실)인 것으로, 컴퓨터로 구현되지 않으면 거짓인 것으로 믿는다. 그런 검정 방법이 가장 ‘과학적’이라고 생각한다.
가장 대표적인 것이 얼마 전에 논쟁이 된 미분에 대한 (컴퓨터) 구현성일 것이다. 물론 요즘은 웬만한 수학 패키지로 미분할 수 있고 결과를 상징적으로 보여주는 소프트웨어가 다수 존재한다. 그렇다고 해서 해석학적 의미의 미분을 완벽하게 구현할 수 있다는 의미는 아니다.
기본적으로 미분은 함수의 연속성에 기반 두고 극한의 개념이 들어가는데, 수학적·해석학적 의미의 연속성이나 극한은 컴퓨터로 구현 및 표현하는 것이 불가능하기 때문이다. 하지만 많은 이가 이것이 가능하다고 이야기한다. 지금 나온 수학 소프트웨어가 이런 계산을 다 해준다는 이유로 말이다.

또 하나의 예는 ‘빅데이터나 데이터 과학이 미래를 예측할 수 있느냐’의 논쟁일 것이다. 데이터 분석은 태생적인 한계로 미래를 예측하는 것이 불가능함에도 코딩하는 많은 이가 이것이 가능하다고 믿는다.
앞으로 코딩이 의무화 되고 어려서부터 코딩만 알고 자란 아이들이 성인이 되면 이런 성향은 더욱 커지고 전반적인 사회 분위기는 더 심해질 것이다. 많은 사람이 문제 해결의 기본 원리를 이해하려고 노력하기보다는 일단 코드로 짜서 구현되는지 먼저 확인할 것이고, 구현되면 구현된다는 이유 하나로 모든 수학적(혹은 과학적) 진실성을 뭉개버릴 것이다.
그런 분위기가 심화될수록 창조적인 인재가 나올 가능성은 더욱 희박하다. 내가 특히 어렸을 때의 코딩 교육을 반대하는 가장 큰 이유도 여기에 있다.
마치며
교육에서 중요한 것은 아이들을 생각하게 만드는 것이다. 단순한 글쓰기보다 문학이 중요하고 단순 계산보다 수학이 중요하다. 과학이 중요하고 예술이 중요한 이유는 ‘무엇’과 ‘왜’를 생각할 수 있는 소재(Resource)를 제공하기 때문이다. 이런 재료 및 소재를 잘 버무려 사용하기 위해 필요한 것은 또 다른 교과 과정이 아니라 기존의 재료를 잘 섞어 스스로 사용하도록 생각할 시간이다.
여건 상 아이들에게 충분한 생각의 시간을 줄 수 없다면 모자란 시간이라도 잘 활용하도록 해주는 것이 지금 할 수 있는 최선의 교육 정책일 것이다. 어쩌면 스스로 생각할 시간을 만들어주는 것이 코딩교육을 의무화 하는 것보다 훨씬 더 필요한 것이 아닐런지.

원문: Amang Kim의 브런치
