
오늘은 보통 통계를 이야기할 때 가장 많이 언급되는 데이터 분석값(혹은 통계값)에 대한 이야기를 하고자 한다.
보통 확률이나 통계의 정확성을 이야기할 때 가장 잘못 이해하고 있는 부분은 ‘데이터 분석의 정확도’일 것이다. 데이터분석(비단 데이터 분석뿐만 아니라 통계모델, 확률모델, 예측모델 등등)의 정확도를 이야기 하는 데 있어서 가장 흔하게 하는 말이 뭐냐면, 실제 해당되는 일이 검색(혹은 발생)되는 경우 데이터 분석이 맞는 것으로, 그렇지 않으면 틀린 것으로 이야기하는 것이다. 이렇게 편협적인 판단은 (미래에)대한 예측 분석의 경우 훨씬 심하다. 다시 한번 말하지만, 모델 자체의 정확도와 실제 사건에 대한 전개 여부는 별개의 문제이다.
어쨌든 오늘은 이에 대한 이야기를 하고자 한다. 이야기를 시작하기 위해 통계에서 말하는 오차범위(혹은 신뢰도, 신뢰구간, 신뢰수준 등등)에 대한 이야기를 우선 이야기해야 할 것 같다.
오차범위는 우리가 목표로 하는(혹은 해solution이라고 생각되는) 값에서 측정했을 때 벗어날 수 없는 범위를 이야기하고, 신뢰구간은 목표로 하는 값이 얼마나 신뢰 가능한지를 확률(혹은 백분율)의 범위 형태로 나타난 값을 의미한다. 따라서 오차범위로 통용되는 숫자는 실수(Real number)이나, 신뢰구간(혹은 신뢰수준)은 음의 수나 1(혹은 100%)를 넘는 수를 가질 수 없다. 하지만, 신뢰구간(신뢰수준)에서의 오차범위는 신뢰구간이 가지는 수의 범위(Range)를 넘지 못한다.
일상생활에서는 신뢰구간과 신뢰구간에서의 오차범위가 많이 알려져 있다. 이러한 신뢰구간이 가장 많이 쓰이는 곳은 선거출구조사와 같은 설문조사일 것이다. 예를 들면 이런 식이다.
이모 후보 60%, 김모 후보 30%, 강모 후보 10%. 이는 95%+/-1.5%의 신뢰구간을 가집니다.
그렇다면 당신은 뉴스에서 저 기사를 보았을 때 어떻게 이해할 것인가? 흔히들 하는 생각은, 통계값을 바탕으로 ‘이모 후보 당선 확실’로 추론할 것이다. 하지만 실제 해석 방법은 ‘선거일에 위의 예측으로 맞출 가능성이 높은가’가 아니라, ‘저 예측이(완전히) 틀리더라도, 틀린 경우를 포함한 통계치의 범위가 신뢰구간을 벗어나지 않는다’는 것을 뜻한다.
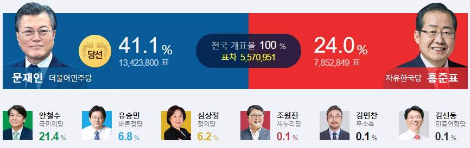
지난 대선을 예를 들어보겠다.
출구조사 결과 문재인 후보가 40%의 득표율로 당선이 예상됩니다. 이 출구조사는 95%+-2.5%의 신뢰도를 가집니다.
이 문장의 의미는 문재인 후보가 당선(가능성)이 확실시된다는 의미가 아니라, 이번에 당선되지 않은 결과를 포함하여 통계를 낼 경우는 92.5%의 가능성으로, 이번에 당선된 결과를 포함하여 통계를 낼 경우는 97.5%의 가능성으로 통계치가 바뀌는 것을 의미한다.
만약 신뢰수준이 99%+-0.5%라면 어떤가? 이번 선거에서 문재인 후보가 당선된다고 볼 수 있는가? 대답은 ‘아니오’이다. 여전히 문재인 후보는 당선이 될 수도, 되지 않을 수도 있다. 다만 당선이 되었을 경우의 신뢰수준은 99.5%, 당선이 되지 않을 경우 98.5%로 신뢰수준이 떨어진다는 것을 의미할 뿐이다. 여기서, 신뢰구간(혹은 신뢰수준)을 구할 때 가장 중요한 문제가 되는 것은 바로 샘플의 크기이다. 샘플의 크기가 작으면 통계값이 사실이라고 하더라도 그 값을 믿을 수가 없다. 그 이유는 오차범위에 따른 변화폭이 너무 크기 때문이다.
데이터 분석의 타당성은 어떤 사건의 결과와 상관없다
너무 어렵고 와닿지 않는가? 그렇다면 확률/통계에서 가장 흔하게 쓰이는 예제인 ‘동전 던지기’로 예를 보여주겠다. 당신은 동전 던지기를 해서 앞면이 나오길 기대하고 있다. 앞서 누군가가 2번의 동전 던지기를 통해 얻은 데이터가 모두 앞면(즉, 100% 앞면)이었다면, 당신은 동전을 던졌을때 앞면이 나올 것이라 확신할 수 있는가?
어쩌면 당신은 앞선 동전 던지기에서 모두 앞면이 나왔으니 당신이 던질 때에도 앞면이 나올 것이라 예상할 수 있을 것이다. 하지만 틀렸다. 적어도 통계적인 방법에서는 말이다. 위의 실험에서 앞면이 나올 가능성에 대한 오차 범위를 생각해보면 100%-33% (100%+33은 100%가 넘으므로 무시), 즉 67%~100%의 오차범위를 갖는다. 동전은 여전히 앞면이 나올 수도 있고 뒷면이 나올 수도 있다. 즉, 당신이 동전을 던졌을 때, ‘앞면이 나온다고 확신할 수 없다’.

다시 한번 동전 던지기를 한다고 하자. 다만 이번에는 앞서 누군가가 200번의 동전 던지기를 통해 얻은 데이터가 있고, 그중 190번이 앞면이었다. 그렇다면 당신이 동전을 던졌을 때, 앞면이 나온다고 확신할 수 있는가? 이에 대한 대답은 역시 ‘확신할 수 없다’ 이다.
물론 오차범위를 보면 매우 적다. 그래서 당신이 시도할 때 앞면이 나올 가능성이 높은 것만은 틀림없는 사실이다. 그리고 조금 더 생각을 발전시킨다면 ‘해당 동전은 편향되어 있다’고 추론이 가능하며, 이러한 추론(혹은 분석)은 타당한 것이다(하지만 당신의 시도에서는 여전히 앞면이 나올 수도 있고 뒷면이 나올 수도 있다).
그런데 만약 같은 조건에서 당신이 실제로 동전을 던졌을 때 앞면이 아닌 뒷면이 나왔다면, 당신의 추론은 틀린 것인가? 당신의 시도에서 설령 뒷면이 나왔다고 하더라도, 기존 데이터(200번 던져서 190번 앞면이 나온) 나 업데이트된 데이터(201번 던져서 190번 앞면이 나온)에 기반한 “해당 동전이 편향되었다”는 추론(분석)은 여전히 타당하다.
즉 당신의 시도에서 앞면이 나왔건 뒷면이 나왔건 상관없이, 데이터분석을 통한 추론은 여전히 유효하다는 말이다. 다시 말해 데이터 분석의 타당성은 어떤 사건의 결과 여부와 상관이 없다. 어떤 사건의 결과 여부는 그다음 사건(즉, 미래) 예측에 대한 오차범위만을 결정할 뿐이다.

많은 사람들이 데이터 분석에 대한 타당성 여부를 사건 결과 일치 여부로 결정하는 경우가 많다. 다시 한번 말하지만, 데이터분석의 타당성은 실제 사건의 결과와 상관이 없다. 예를 들어 어떤 빅데이터 회사, 혹은 빅데이터 분석 전문가가 자기네 데이터 분석 방법이 얼마나 월등한지를 설명한다고 하자. 이걸 동전던지기로 예를 든다면 이런 식이 될 것이다.
우리가 (빅)데이터 분석을 해보니, 이번 시도에서는 뒷면이 나온다고 했는데 실제 그 사건에서도 뒷면이 나왔다. 그러니 우리의 데이터 분석 방법이 맞는 거다.
당신의 생각은 어떤가? 위와 같은 방식의 논리 전개가 왜 말이 되지 않는지 촉이 온다면, 오늘 나의 글쓰기는 성공한 거다.
원문: Amang Kim의 브런치
