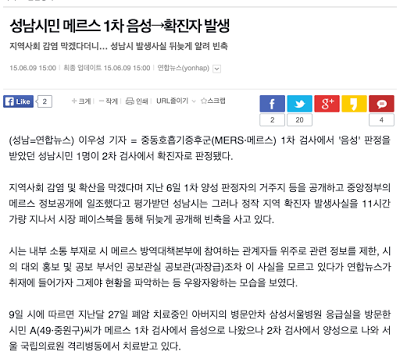
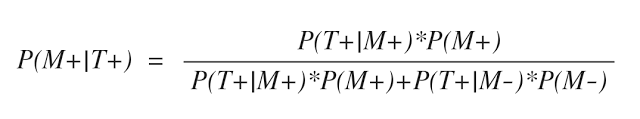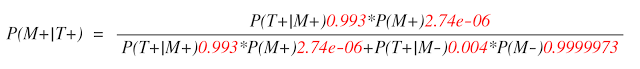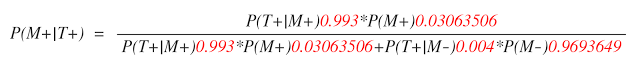메르스 확산이 이슈인 가운데, 메르스 검사 과정 중 오락가락 하는 검사 결과에 혼란이 가중되고 있는 상황이다. 관련 기사를 보면, ‘양성->음성->양성’ 의 경우, 성남 초등학생의 경우 ‘음성->양성->음성’ 으로 메르스 검사 결과가 왔다 갔다 하며, 메르스 양성인지 음성이지 확진을 못하고 있는 상황이 발생하고 있다.
메르스 검사 정확도: 완벽하진 않아도 정확한 편
현재 보건복지부에서 공시한 메르스 검사 방법은 아래와 같다.
real time RT-PCR라는 방법으로, 메르스 원인 바이러스의 특정 유전자 영역을 검사하는 방법이다. 이 방법은 연구 목적으로 출시된 제품들로 메르스 확산이라는 국가적 비상사태를 기해, 특별히 임상 진단 목적으로 사용되고 있다.
원래대로라면, 검사의 정확도(민감도Sensitivity; 양성을 실제로 양성이라 잘 맞추는 정도, 특이도specificity; 음성을 실제로 음성이라 잘 맞추는 정도)에 측면에서 신뢰도 있는 연구 결과가 제출되고 이를 식약처에서 승인을 해야 인간을 대상으로한 임상 검진 키트로 활용할 수 있다.
현재 사용되는 메르스 검사의 정확도를 알 수 없지만, 낙타의 메르스 바이러스를 검진하는 진단 키트를 개발해 정확도를 측정해 논문으로 출판했던 고려대 송대섭 교수팀의 경우, real time RT-PCR 기반 메르스 검사 진단 방법의 정확도는 민감도 Sensitivity 93.9%, 특이도 Specificity 99.6% 에 이르러 비교적 높은 정확도를 보였다.
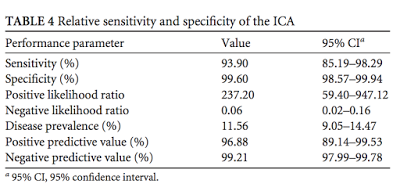
인간을 대상으로 한 검사 정확도 측정은 아니었지만, real time RT-PCR 을 기반으로한 메르스 바이러스 검사의 정확도는 대동소이할 것이라 보면, 현재 국내에서 메르스 감염의심자를 대상으로 수행되는 검사 정확도도 이와 비슷하리라고 예상해 볼 수 있다.
메르스 검사 정확도에 대한 이해: 우리의 직관과 어긋나는 이유
검사 정확도는 민감도(Sensitivity)와 특이도(Specificity)라는 기준으로 측정한다. 메르스 검사에서 민감도는 메르스 바이러스가 있을 때 검사 결과 양성일 확률을 이야기 한다. 특이도는 바이러스가 없을 때, 검사 결과가 음성일 확률이다.
수식으로는 아래와 같이 표현한다.
메르스 검사 민감도( Sensitivity) = P( test+ | mers+ ) = 93.9%
메르스 특이도( Specificity) = P( test- |mers- ) = 99.6%
자, 여기서 부터가 문제다. 민감도 93.9%, 특이도 99.6%의 정확도를 가진 검사를 이용해 메르스 감염의심자를 검사했을 때, 양성 결과가 나왔다. 이 때, 이 감염의심 환자가 진짜 메르스 환자일 확률은 얼마일까?
이는 베이시안 확률 계산을 통해 구할 수 있는데, 통계학 교과서의 앞부분에 소개되는 아주 기본적인 부분이다. 하지만, 이를 ‘정확히’ 이해하고 있는 사람 또한 그리 흔치는 않은데, 이는 다소 직관과 배치되는 계산 결과로 기인하는 부분이 크다. 특히 빈도가 낮은 ‘사건’에 대한 베이시안 확률 계산을 통해 얻어지는 사후확률 결과는 직관과 매우 배치된다.
‘메르스 감염’ 이란 사건은 어떨까? 체감으론 엄청나게 확산되는 것 같지만, 실제론 우리나라 5천만명 중 현재(2015년 6월 13일) 까지 확진자가 137명인 매우 희귀한 사건이다. 다시 말하면, 메르스 검사도 빈도가 매우 낮은 사건을 확인하는 검사로 사후확률이 우리의 직관과 매우 배치 될 수 있다는 말이다.
메르스 검사 양성일 때, 실제 메르스 환자일 확률은 얼마나 될까?
그럼 메르스 검사 결과 양성인 경우, 실제 환자가 메르스 바이러스에 감염되었을 확률을 구해보자. 이를 구하는 수식은 아래와 같이 쓸 수 있다. ( M = Mers, T = Test )
검사 결과가 양성( T+) 인 경우, 메르스 환자( M+) 일 확률은, 검사 민감도: P(T+|M+), 메르스 유병률( Prevalence) : P(M+) , 검사 특이도: P(T-|M-) 값이 주어지면 구할 수 있다. ( P(T+|M-) = 1-P(T-|M-) = 1-specificity )
검사 민감도와 특이도는 위에서 언급되었듯 93.9%, 99.6% 를 대입하면 되는데, 메르스 유병률은 어떤 수치를 써야 할까가 이슈다.
우리 나라 전체 메르스 유병률은 137 / 5천만 = 0.00000274 로 매우 희귀한 사건이 된다. 메르스 감염의심자라는 메르스 고위험군으로 좁히면 이 집단에 대한 유병률은 137 /4472 (자료 참조: 메르스 정보 포털) = 0.03063506 로 약 3% 정도로 높아진다.
여기서는 일반 국민, 메르스 감염의심자 두가지 집단에 대한 유병률을 각각 적용해 P(M+|T+) 확률을 모두 구해 보자.
1. 일반 국민 ( 메르스 저 위험군)
위의 수식에 각각의 수치를 대입하면 아래와 같다. ( 붉은 색 수치가 왼쪽 수식에 해당하는 확률 )
계산해 보면 검사 양성일 때, 메르스 환자일 확률은 P(M+ | T+ ) = 0.0006428033, 즉 0.064%로 엄청나게 낮다. 즉, 메르스 위험도가 낮은 일반 국민을 대상으로 검사를 수행해 양성이 나왔을 때, 메르스 환자로 확진하는 건 불가능 하다.
2. 메르스 감염의심 환자 ( 메르스 고 위험군)
마찬가지로 수식에 수치를 대입해 보면 아래와 같다.
메르스 감염의심 환자에 대해 검사 양성일 때 메르스 환자일 확률 P(M+|T+) = 0.881219, 즉 88.12%로 상당히 높은 신뢰도로 메르스 환자임을 의심해 볼 수 있다.
(베이시안 정리에 익숙하지 않으신 분들은 위의 확률 계산 자체를 쉽게 이해하기 어려울 수 있다. 이런 경우 자연빈도법으로 나타내면 쉽게 이해할 수 있는데, 인하대 의대 황승식 교수님께서 위의 계산 내용을 자연빈도법으로 정리해 공유해 주셨기에 아래에 이를 추가로 공유 합니다. )
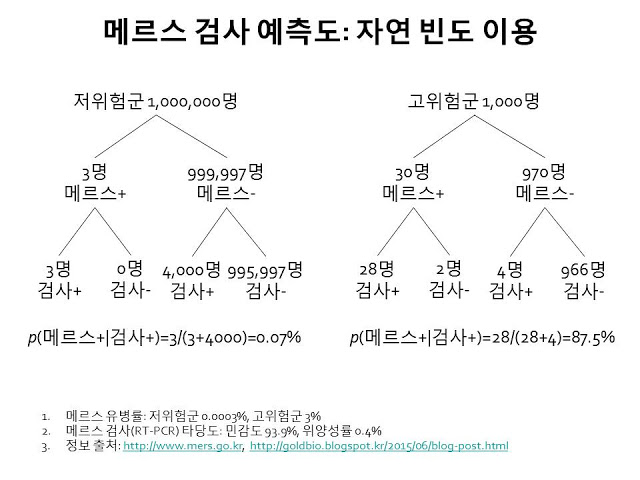
계산된 검사 결과 메르스 양성 확률은 베이시안 확률론에 대한 이해가 없는 사람에게는 아마도 직관과 매우 어긋나 보일 거라 본다. 검사 민감도 93.9%, 특이도 99.6% 짜리 검사를 수행해 검사 결과 양성이 나와도, 일반인은 겨우 0.064%, 메르스 의심 환자의 경우 88.12% 밖에 안 된다니. 하지만, 이것이 바로 희귀한 질병 검사 방법을 통해 우리가 통계적으로 신뢰할 수 있는 한계다.
검사 정확도가 100%가 되지 않는 한, 희귀 유병률의 질병/바이러스 검사를 통해 100% 확진을 결정지을 수 없는 것이 현실이다. 검사 정확도가 99%를 넘어가는 매우 신뢰도 높은 검사라 하더라도 위의 일반국민 메르스 유병률( 0.00000274) 처럼 매우 희귀한 케이스를 한번의 테스트로 확진해 낼 수 없다.
요즘 주변에 원하는 사람은 누구든 ‘메르스 검사’를 해주면 되지 왜 안 해주고, 문진과 진찰을 통해 메르스 고위험군으로 분류된 사람만 검사를 해주느냐고 불평하는 경우가 많다. 바로 이게 이유다.
메르스 저위험군인 일반인에 대한 메르스 검사 1번으로 메르스 바이러스를 가지고 있는지 알 수가 없다. 이들은 검사 결과 양성이 나와도 메르스 바이러스를 가졌을 확률은 1%도 안 되는 테스트를 받을 필요가 없다.
메르스 고위험군인 감염의심자에게 수행한 후, 양성인 경우 88.12% 로 메르스를 의심해 볼 수 있다. 중요한 것은 이 경우에도 100%가 아니라는 점. 이것이 바로 메르스 확진을 위해 반복적으로 메르스 검사를 수행하는 이유다.
메르스 검사 결과 양성과 음성이 혼재된 경우의 확률 계산
베이시안 확률은 ‘사전 확률’이 ‘사건에 대한 관찰’ 결과에 따른 ‘사후 확률’을 계산한다. 메르스 검사를 수행할 때 검사 대상자가 메르스 환자일 것이라 예상하는 확률이 바로 사전 확률이 된다. 검사 대상자가 일반인이라면, 전체 국민 대비 메르스 유병률을 근거로 검사 대상자가 메르스일 확률을, 검사 대상자가 메르스 감염 의심자라면, 감염 의심자들 대비 메르스 유병률( 3%)를 근거로 이 사람의 메르스 확률을 가늠할 수 있다.
여기서 메르스 검사를 수행 결과 양성이 나왔다. 사전 확률로 메르스 환자 확률을 가늠하다가 검사 결과 양성이라는 사건을 관찰하고 난 이후, 메르스 환자 확률은 더 높은 확률로 조정된다. 이것이 ‘사후확률’이다.
메르스 검사를 1번 수행한 후, 우리는 검사 받은 환자의 메르스 확률을 ‘사후확률’로 조정했다. 이 환자에 대해 메르스 검사를 한 번 더 수행한다면 어떻게 해야 할까? 두 번째 검사 시작 시, 우리는 이 환자가 메르스 환자일 확률을 첫번째 검사 이후 사후확률로 의심할 수 있다. 즉, 두번째 메르스 검사 시 ‘사전확률’은 첫 번째 검사 후 ‘사후확률’로 놓고 계산하면 된다.
그러면, 글의 맨 처음으로 돌아가 ‘양성’과 ‘음성’이 반복된 경우 환자들에 대한 메르스 확률을 구해보자. 두 경우 모두 ‘감염의심자’로 최초의 검사 시 사전확률은 3%(0.03063506 ) 로 놓고 계산한다.
1. ‘양성->음성->양성’ 인 경우 메르스 환자일 확률
첫번째 결과 양성 후 : 0.881219, 88.12%
두번째 결과 음성 후 : 0.312416, 31.24%
세번째 결과 양성 후 : 0.9907117 , 99.07%
이 환자의 경우 4번째 테스트 양성이 나오는 경우 메르스 환자일 확률은 0.9999601 , 99.99%로 메르스 환자일 확률이 매우 높다. 음성인 경우에도 여전히 0.8672425, 86.72% 확률로 메르스 환자일 가능성이 높다.
2. ‘음성->양성->음성’ 인 경우 메르스 환자일 확률 (성남 초등학생)
첫번째 결과 음성 후: 0.0019318, 0.19%
두번째 결과 양성 후: 0.312416, 31.24%
세번째 결과 음성 후 : 0.02707433 , 2.7%
성남 초등학생의 경우 4번째 검사 후 음성인 경우, 메르스 환자일 확률은 0.00170141 , 0.17% 로 메르스 환자일 가능성이 매우 낮다. 하지만, 양성인 경우 0.8672431 , 86.72%로 메르스 환자일 확률이 다시 높아진다.
베이시안 확률 계산을 이용해 검사 결과에 따른 메르스 확진 확률을 계산하면, 매 검사 시마다 확률이 뒤바뀐다. 질병관리본부의 메뉴얼은 어떻게 메르스 확진을 결정짓도록 되어 있을까? 인터넷 검색을 열심히 해봤지만, 질병관리본부의 지침은 특별히 발표된 내용이 없는 것 같다.
2015년 6월 13일 오후 3시 자로 아래와 같은 기사가 올라왔다. 요약하면, 1차 음성-> 2차 양성 인데 메르스 환자로 확진하고 치료를 받고 있다는 것이다.
‘음성->양성’인 경우 위에 소개한 베이시안 확률 계산법으로 메르스 환자일 확률을 계산해 보면 겨우 31.24% 밖에 안 된다. 근데 어떻게 메르스 환자로 확진했을까? 위의 확률 계산에서 P(M+) 즉 메르스 유병률은 집단별로 더 세분해 구분할 수 있다.
이 환자의 경우 49세로 메르스 감염위험군에서 확진판정을 받을 가능성이 높은 집단이라는 점 등을 고려해 좀 더 자세한 확률 계산을 통해 2번의 검사 결과(음성->양성)로도 확진 판정을 받았을 가능성이 있다.
혹은, 2번의 검사 중 한번 양성이 나왔고, 환자의 상태를 진찰한 결과 메르스 환자의 소견을 보인 경우, 확률적으로 메르스 확률일 가능성이 낮아도 메르스 환자로 확진하고 치료에 돌입했을 수 있다.
정부가 메르스와 관련된 모든 정보를 신속히 공개하겠다고 했는데, 검사 결과 확진 판정에 대한 기준이나, 자세한 메르스 확진자 정보(de-identified된 명단과 관련 정보) 등을 공개 한다면, 수많은 역학, 통계 전문가나 개발자들이 메르스 확산 방어에 도움이 되는 다양한 분석과 툴들을 개발해 메르스 확산을 방지하는데 큰 도움을 줄 수 있다. (이미 눈에 띄는 몇몇 툴들이 개발되어 있다)
전세계 어느 나라든, 전염병 확산, 재난 등이 닥쳤을 때, 신속히 관련 정보들을 광범위하게 공개하고, 전문가들이 이를 활용할 수 있게 만든다면 재난과 전염병 확산 등을 빠르게 극복해 내는데 큰 도움이 된다. 그런 시대다 지금이.
IT 강국이라고 말만 떠벌리지만, 메르스 감염 정보 포탈도 그렇고, 정보 공개 수준이나 방법 등이 너무 시대에 뒤떨어지는 것 같아 답답하다. 정부 포탈 보단 KBS의 데이터저널리즘 팀이 구축한 메르스 정보 페이지가 정보의 양과 질 모두 월등히 나은 정보를 제공하고 있다(최신 data visualization tool인 Tableau 사용).
아무튼, 별거 아닌 이 글도 메르스 감염에 대한 걱정에 떨고 있는 누군가에게 도움이 되기를 바라며 글을 마친다.