※ Jana Vembunarayanan의 『How to lie with statistics』을 번역한 글입니다.
거짓말에는 세 종류가 있다. 거짓말, 빌어먹을 거짓말, 그리고 통계다.
- 벤저민 디즈레일리
대럴 허프(Darrel Huff)의 책 『새빨간 거짓말, 통계(How to lie with statistics)』은 1954년 처음 출간되었다. 하지만 그 내용은 오늘날에도 아주 잘 적용되며, 언론, 정치인 그리고 기타 다른 이들이 어떻게 통계를 사용해 무비판적인 독자들을 속일 수 있는지 설명해준다.
1. 편향된 샘플
《리터러리 다이제스트(Literary Digest)》는 미국에서 인기 있는 매거진이었다. 이 매거진에서는 1936년 대통령 선거 전 1천만 명의 독자들을 대상으로 누구에게 투표할 것인지 전화 설문조사를 실시했다. 설문 조사 결과, 랜든이 370표, 루스벨트가 161표를 받는 것으로 나왔다.
하지만, 실제 결과는 완전히 달랐다. 랜든이 8표를 얻었고, 루스벨트가 523표를 얻었다. 설문 조사가 왜 틀린 것일까? 그 당시에 전화는 부유층의 전유물이었고, 이들은 공화당의 린든을 선호했던 것이다. 선택한 샘플이 전체 미국인들을 대표하지 못 했던 것이다. 편향된 샘플의 사례였다.
샘플이 예측성을 얻기 위해서는 1) 전체 인구를 대표해야 하며, 2) 모집단은 전체 인구에서 무작위로 선택되어야 한다.
2. 평균의 함정
부시 행정부가 세금 감면 계획을 내놓은 적이 있다. 이 계획이 실현되면, 미국 가정의 평균 세금 감면 혜택이 1,083달러에 이를 것이라고 주장했다. 하지만, 미국 가정 중 50% 이상이 단 100달러로 세금 감면 혜택을 보지 못 했다. 부시 행정부가 거짓말을 한 것일까?
그렇지 않다. 행정부가 주장한 1,083달러는 평균값이었고, 이상치에 의해 왜곡된 것이었기 때문에, 이 수치가 대부분의 가정에 적용되지 못했던 것이다. 중간값은 100달러 미만이었다. 평균은 자격을 갖춰야 한다. 그렇지 못한 경우, 보고된 수치는 큰 가치를 얻을 수 없게 된다.
때로는 자격을 갖춘 평균도 위험하다. 평균 4피트 깊이의 수영장에서 키 6피트인 사람이 익사했다. 어떻게 가능할까? 수용장 깊이의 범위가 3피트에서 10피트 사이였기 때문이다. 아래 그림이 평균의 3가지 경우를 명확하게 설명해 준다.
3. 작은 샘플이 극단적인 결과를 가져올 수 있다
공정한 동전 던지기를 하면, 앞면이 나올 확률은 1/2이다. 하지만 동전 던지기를 5번 하면, 모두 앞면이 나올 수도 있다. 그럼에도 동전 던지기를 훨씬 더 많이 한다면, 실제 결과는 1/2의 확률에 수렴하게 된다.
가장 좋은 학교는 평균적으로 소규모 학교였다는 연구가 있었다. 이 데이터를 바탕으로 게이츠 재단은 소규모 학교 설립에 상당한 투자를 했다. 그렇다면, 소규모 학교가 정말로 더 나았을까? 그렇지 않았다. 게이츠 재단에 보고한 통계학자에게 가장 안 좋은 학교의 특성에 대해 물어 봤더니, 안 좋은 학교 또한 평균보다 소규모인 경향이 있었다.
진실은 소규모 학교가 평균보다 나을 것이 없었다. 이들은 단순히 더 다양했을 뿐이다. 작은 샘플에서 얻은 결과는 극단적인 결과일 수 있기 때문에, 거기에 의존해서는 안 된다.
4. 그래프와 그림
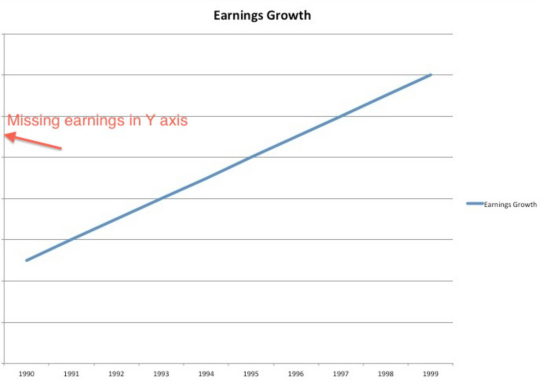
아래 차트는 한 기업의 1990년부터 1999년까지 수익 성장세를 나타낸 것이다. 이 차트는 이 기업의 수익이 폭발적으로 성장했음을 보여준다. 실적 수치에는 세로축이 빠졌다. 의도적으로 빼본 것이다.
1990년 수익을 1달러로, 1999년 수익률 1.1달러로 그린 것이다. 10년 동안 수익 성장률은 단 0.96%에 불과했다. 어떤 그래프를 볼 때, 세로축과 가로축 모두가 표현돼 있는지 확인해야 한다.
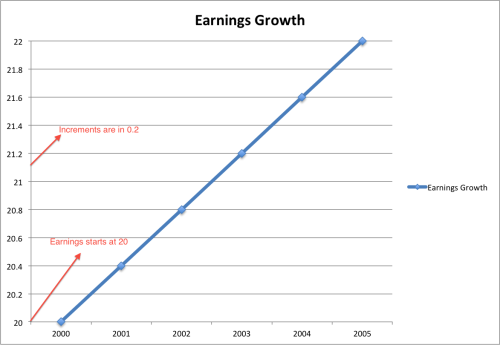
같은 기업의 2000년-2005년 수익 성장세를 살펴보자. 6년 동안 수익은 20달러에서 22달러고 성장했다. 연평균 성장률은 1.60%로 그리 큰 것이 아니다. 차트는 아주 편평해 보인다.
같은 데이터를 사용해 차트를 다시 그려보았다. 아주 폭발적으로 보인다. 어떻게 이런 일이 가능한 것일까? 차트를 0달러 대신 20달러부터 시작하고 세로축의 증분을 0.2로 했기 때문에, 엄청난 성장을 한 것 같은 환상을 만들어 낸 것이다. 어떤 차트를 볼 때, 시작 값과 증분에 주의해야 한다.
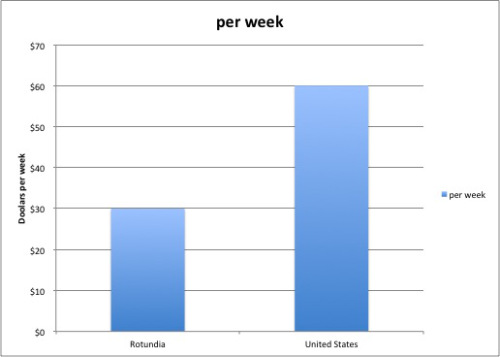
미국에서 목수의 평균(중앙값) 주간 임금이 60달러이며, 로툰디아에서는 30달러라고 가정해 보자. 이 데이터를 나타낸 막대그래프는 분명하게 이 사실을 보여주고 있다. 미국의 막대 높이가 로툰다이의 두 배다.
이 이야기를 좀 더 극적으로 보이고 싶다면, 그림으로 표현하면 된다. 아래 그림은 우리에게 미국이 로툰디아보다 훨씬 더 잘 산다는 인상을 준다. 그 이유는 무엇일까? 미국의 그림 높이는 2배인 것은 맞다. 하지만 미국의 그림 폭 또한 2배로 늘어났다.
따라서 이 그림은 미국이 로툰디아보다 8배 더 잘 산다는 환상을 가져다준다. 왜 8배인가? 부피는 한 변 X 3이기 때문이다. 그림을 볼 때, 폭이 변하지는 않았는지 확인해야 한다.
5. 반쪽짜리 수치
자신이 입증하고 싶은 것을 입증할 수 없을 경우 뭔가 다른 것을 보여주고 같은 것인 양 할 수 있다. 예를 들어 여러분이 감기를 치료약을 발명했다고 해보자. 하지만 입증할 방법이 없다. 어떻게 해야 할까?
그 약을 투여한 시험관에서 3만 2,868마리의 세균이 죽었다는 보고서를 내놓고, 이 보고서를 공공 기관에서 인증받으면 된다. 그리고 그 약이 시험관에서 세균을 죽였고, 따라서 감기도 치료할 거라고 광고하면 된다. 잊지 말고 주장하는 것과 판매되는 것 사이의 관계에 의문을 제기해 봐야 한다.
6. 상관관계는 인과관계를 설명해주지 못한다
두 변수 사이의 상관관계는 인과관계를 설명할 필요가 없다. 이런 뉴스 제목을 보자. “병에 든 생수를 마신 아이들이 더 건강하다.” 이 말이 정말 사실인가? 떠올려야 할 의문은 “누가 생수를 구입했는가?” 하는 것이다. 부모가 부자라면 생수를 마시고, 아이들이 건강할 가능성 모두 다 높다.
뉴헤브리디스(호주 북동 남태평양상의 군도) 사람들은 몸에 이가 있어야 건강하다고 믿었다. 이 사람들이 몇 세기 동안 경험한 바, 건강한 사람들은 일반적으로 몸에 이가 있었고, 아픈 사람은 거의 그렇지 않았다는 것이다. 실제 이유는 무엇일까? 아픈 사람은 열이 있고, 따라서 몸이 너무 뜨거워진다. 이가 뜨거운 몸에는 살지 않기 때문에 아픈 사람에게는 이가 없는 것이다.
맺음말
통계는 유용한 도구다. 아마존, 넷플릭스, 페이스북 같은 사이트는 우리가 좋아하는 품목을 예측하기 위해 통계를 이용한다. 하지만 어떤 유용한 도구와 마찬가지로 통계도 오용될 수 있다. 통계가 진실인지 거짓인지 알아내는 것이 우리가 할 일이다. 앞으로 어떤 통계 정보를 접하더라도 이런 생각을 해봐야 한다.
- 누가 그 통계를 내놓았고, 또 그 동기는 무언가?
- 어떤 방법으로 통계를 냈는가?
- 앞뒤가 맞는 통계인가?
원문: 책도둑 &