※ Of Dollars and Data의 「Wanna Get Rich? Think Fractally」를 번역한 글입니다.
복리의 프랙털 특징에 대해
이 글에서는 복리, 프랙털 그리고 부자가 되기 위해 이들을 사용할 방법을 논의해 본다. 복리를 다루기에 앞서 프랙털에 대해 알아보자. 프랙털이란 상이한 크기(또는 배율 수준)로 대칭성을 표시하는 기하학적 개체를 말한다.
프랙털을 시각적으로 확대하면 기존의 (더 큰) 객체와 비슷한 패턴을 보게 된다. 아래 시어핀스키 삼각형(Sierpinski Triangle)은 외부의 삼각형 패턴이 그 안에서 무한히 반복되는, 프랙털을 설명하는 데 가장 직접적인 방법 중 하나이다.
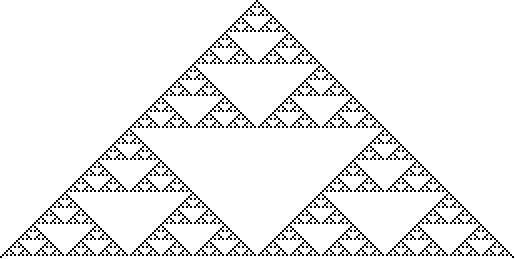
프랙털의 특징은 자연 속에서 거의 모든 곳에서 발견된다는 것이다. 나무, 해안선, 정맥 그리고 다른 많은 자연 물체가 프랙털 속성을 나타낸다. 재미있는 프랙털 중 하나가 로마네스코 브로콜리(Romanesco Broccoli)다.

도대체 프랙털이 어떻게 부자로 만들어 줄 수 있단 말인가? 프랙털 자체는 아무것도 해 주지 못한다. 하지만 복리와 복리의 프랙털적 움직임을 이해하면 부자가 될 수 있다. 우선 아래의 사고 실험을 고려해 보자.
100달러를 투자하기로 결정했고 10%의 연간 수익률을 올릴 수 있다고 가정한다. 1년이 지나면 원금 100달러와 이자 10달러를 갖게 될 것이다. 특별한 것은 없다. 하지만 이 돈을 계속해서 복리로 늘리게 되면 그 과정은 프랙털처럼 움직이기 시작한다. 2년 차가 되면 100달러에 다시 10달러의 이자가 붙고, 1년 전의 이자 10달러에 다시 이자 1달러가 붙는다. 10달러가 1년 전의 100달러처럼 행동하기 시작한 것이다.
10달러와 그 이자 1달러의 관계는 100달러와 그 이자 10달러의 관계와 같다. 이 과정은 3년 차에도 2년 차의 1달러에 다시 0.1달러의 이자가 붙는 것처럼 계속된다. 복리의 아름다움은 계속해서 프랙털처럼 행동한다는 것이다. 각각의 이자가 다시 이자를 낳는다. 돈이 돈을 벌어오고 결국 부자가 되는 것이다. 이해를 쉽게 하기 위해 복리의 프랙털 같은 특성을 나타낸 아래 그림을 보자.
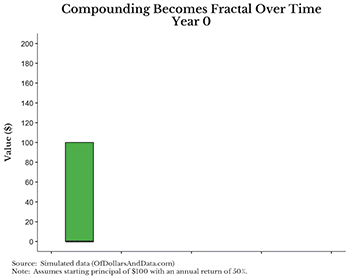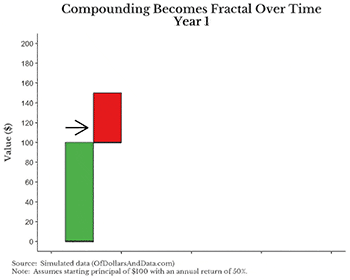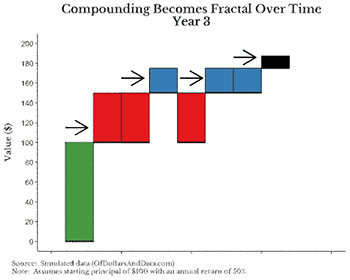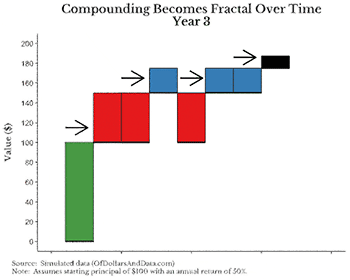
보기 쉽게 연간 수익률을 50%로 했지만 효과는 동일하다. 그림에서 주목해야 할 점은 연도가 지날수록 100달러의 기본 원금(녹색 막대)가 매년 이자(적색 막대)를 벌어들인다는 것이다. 또한 1연차의 이자(적색 막대)가 2년 차부터 이자(청색 막대)를, 마지막으로 2년 차의 이자(청색 막대)도 3년 차부터 이자(흑색 막대)를 만들어낸다.
이 과정에서 놀라운 점은 그 성장세가 엄청나다는 것이다. 기간을 3년만 나타냈지만 더욱 연장하면 당장 그림이 너무 커질 것이다. 이것이 프랙털인지 모르겠다면, 1년 차에서 녹색 막대와 적색 막대 사이의 관계를 보라. 그리고 이 과정은 3년 차 이후에도 계속 반복된다.
프랙털의 힘에 대해 아직도 회의적인가? 앨버트 아인슈타인은 우주에서 가장 강력한 힘이 무엇이냐는 물음에 “복리”라고 대답했다.
프랙털의 진정한 힘
프랙털의 진정한 힘은 몇 가지 단순한 움직임에서 나온 복잡성이 계속해서 반복된다는 사실에 있다. 이것이 자연의 힘과 아름다움이다. 충분히 분열된 세포 덩어리가 인간이 된다. 이 원리는 금융 생활에도 해당된다.
몇 가지 간단한 행동을 계속 반복함으로써 부자로 가는 길이 보장된다. 이렇게 생각해 보자. 저축, 투자, 주기적 재조정을 반복하면 부자가 된다. 하나의 간단한 행동을 여러 번 반복하면 강력한 결과를 얻을 수 있다.
프랙털의 발명가 브누아 망델브로(Benoit B. Mandelbrot)의 멋진 이야기를 남기고 싶다. 망델브로는 1970년대 후반 컴퓨터를 이용해 역대 가장 유명한 프랙털인 망델브로 집합(Mandelbrot set)을 만들었다. 또한 『금융 시장의 이상행동(Misbehavior of Financial Markets)』에서 금융 시장과 유가증권 가격 결정에 정규 분포에 의존하는 행동을 통렬히 비판했다.
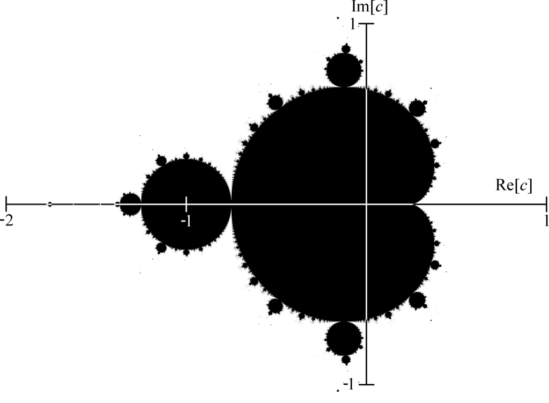
그의 명민함을 보여주는 가장 놀라운 사례는 중간 이름에 있다. 태어날 당시 중간 이름이 있었다는 기록은 없지만 인생의 어느 시점에서 “B”라는 중간 글자를 이름에 넣기로 결정한 것 같다. 누구도 “B.”가 무엇을 의미하는지 몰랐지만 “Benoit B. Mandelbrot”을 의미한다는 이론이 있다. 그렇다, 그의 이름조차 프랙털이었던 것이다.
프랙털에 대해 더 자세히 알고 싶다면 망델브로의 『자연의 프랙털 기하학(The Nature of Fractal Geometry)』을 추천한다.
원문: 피우스의 책도둑 &
